
今回のテーマは小児の薬用量。
小児薬を調剤、監査している時よく遭遇するのがこのシーン。
添付文書に小児薬用量が記載されていない!
慌てることなかれ。
そんな時は小児薬用量を換算する計算式を利用すれば問題ありません。
小児薬用量の計算式は主に5つ存在します。
今回は5つの計算式を紹介していき、
「どの計算式が実用的でおすすめなのか?」
「それぞれの計算式でどれぐらいの差がでるのか?」
などを検証していきたいと思います。
5つの計算式を紹介
① Von Harnack(フォン・ハルナック)の換算表 おすすめ度:★★

かなりざっくりとした換算表となります。大きな欠点として、抜けている年齢も多いため、この換算表だけに頼るのはかなりリスキーと言えるでしょう。しかも7.5歳てまた半端な。。あくまでも参考程度の使用をおすすめします。
② Crawford(クロフォード)の式 おすすめ度:★★

5つの計算式の中で一番正確な薬用量を計算することができるでしょう。
しかし、大きな欠点としては体表面積が必要な点です。
まず体表面積の計算式は非常に複雑です。
体表面積=体重【kg】の0.425乗×身長【cm】の0.725乗×0.007148
とても覚えきれるものではありません。。(※上記はDubois式)
計算ツールが載っているページのリンクを貼っておきます。
また、体表面積を計算するには身長と体重が必要となります。
「体重はわかるけど身長は今いくつだろう?」
というお母様、お父様も多いでしょう。
現実的に現場で使えるかというと微妙なところです。
③ Augsberger(アウグスベルガー)の式 おすすめ度:★★★
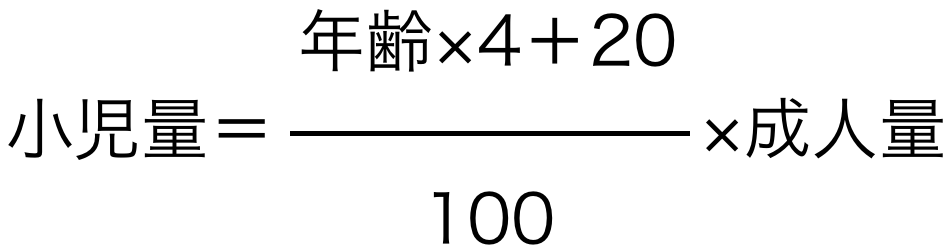
恐らく5つの計算式の中で一番多く使われているのがこちらの計算式でしょう。
多くの小児科医や薬剤師が使用していると思われます。
小児薬用量で有名なこちらの本もAugsberger(アウグスベルガー)の式を参考に小児薬用量が記載されています。

薬剤師の目線から言うと、体重を使わない計算式のため、処方箋を見た瞬間に計算することができ、薬用量が適正か判断することができる便利な式です。
④ Young(ヤング)の式 おすすめ度:★

古くから存在する式で、薬用量が少し少なく計算されてしまうということもあり、現在はほとんど使われておりません。
⑤ Clark(クラーク)の式 おすすめ度:★

この式の欠点は体重をポンドで計算する必要があること。こちらも現在はほとんど使われておりません。ちなみに1ポンドは、0.454kgです。
各計算式でどれぐらいの差がでるのか?
今回は添付文書に小児薬用量が記載されていないポララミンシロップで見ていきたいと思います。年齢、身長、体重は下記に設定します。
年齢:3歳
身長:90cm
体重: 13kg
体表面積:0.558m2(DuBois式で計算)
ポララミンシロップの成人量:1回5mLを1日1〜4回
Von Harnack(フォン・ハルナック)の換算表
計算すると1回1.66...mL。該当する年齢だった場合、一瞬で計算できるのはこの換算表の良いところです。
Crawford(クロフォード)の式
計算すると1.61...mL。この値が一番正確な小児用量と言えるでしょう。
Augsberger(アウグスベルガー)の式
計算すると1回1.6mL。Crawford(クロフォード)の式とほぼ同じ値が算出できました。
Young(ヤング)の式
計算すると1回1mL。やはり他の計算式より少し少なめになるようです。
Clark(クラーク)の式
計算すると1回0.954...mL。こちらも他の計算式より少なめになるようです。
最後に
一番正確な小児薬用量がCrawford(クロフォード)の式から算出された1.61...mLだとすると、この数字に近い値を算出できているのはAugsberger(アウグスベルガー)の式から算出された1.6mLです。
以上の結果から、
計算も簡単で正確な薬用量を計算することができる、
Augsberger(アウグスベルガー)の式が一番実用的と言えるでしょう。
ではまた。